How long does a typical A/B test run for? What percentage of A/B tests result in a ‘winner’? What is the average lift achieved in online controlled experiments? How good are top conversion rate optimization specialists at coming up with impactful interventions for websites and mobile apps?
This meta-analysis of 1,001 A/B tests analyzed using the Analytics-Toolkit.com statistical analysis platform aims to provide answers to these and other questions related to online A/B testing. The layout of the presentation is as follows:
- Background and motivation
- Data and methodology
- Basic test characteristics
- Advanced test parameters
- Outcome statistics
- Efficiency of sequential testing
- Takeaways
Those interested in just the main findings and a brief overview can jump straight to “Takeaways”.
Background and motivation
A/B tests, a.k.a. online controlled experiments are the gold standard of evidence and risk management in online business. They are the preferred tool for estimation of the causal effects of different types of interventions, typically with the goal of improving the performance of a website or app, and ultimately of business outcomes. As such, the role of A/B tests is primarily as a tool for managing business risk while addressing the constant pressure to innovate and improve a product or service.
Given this gatekeeper role, it is crucial that A/B tests are conducted in a way which results in robust findings while balancing the business risks and rewards from both false positive and false negative outcomes. A 2018 meta analysis [1] of 115 publicly available A/B tests revealed significant issues related to the planning and analysis of online controlled experiments. Namely, the majority of tests (70%) appeared underpowered, raising questions related to both unaccounted peeking and to low statistical power. The first can result in inflated estimates and lack of control of the false positive rate, whereas the second can result in failure to detect true improvements and missed opportunities to learn from tests due to underwhelming sample sizes.
Addressing such issues and promoting robust statistical practices has been a major driver behind the development of the A/B testing statistical tools at Analytics Toolkit since its launch in 2014. In 2017 a sequential testing methodology (AGILE) was proposed and implemented to address the motivations behind peeking in a way that provides efficiency and improves the ROI of testing without compromises to statistical rigor. In late 2021 an overhauled platform was released with one aim being to address the second of the major contributors to the poor outcomes of A/B testing efforts – inadequate statistical power. Other goals of the overhaul include prevention or minimization of other common mistakes in applying statistical methods in online A/B tests.
In light of the above, the current meta analysis has a number of goals:
- To provide an outcome-unbiased analysis, improving on the previous study which likely suffered from selective reporting issues.
- To produce a more powerful, and therefore more informative analysis.
- To check the real-world performance of sequential testing which by its nature depends on the unknown true effects of the tested interventions.
- To uncover new insights about key numbers such as test duration, sample size, confidence thresholds, test power, and to explore the distribution of effects of the tested interventions.
- To examine the extent to which the Analytics Toolkit test planning and analysis wizard may encourage best practices in A/B testing and mitigate the issue of underpowered tests.
Data and methodology
The data in this analysis comes from a sample of 1,001 tests conducted since the launch of the new Analytics Toolkit platform in late 2021. The dataset contains both fixed sample tests and sequential tests (AGILE tests), with 90% of tests being of the latter type.
The initially larger sample of tests was screened so that only tests from users who’ve conducted more than three A/B tests in the period are included. The rationale is to minimize the proportion of tests from users without sufficient experience with the platform as well as ones entered while exploring the functionality of the software as such tests might contain questionable data.
46 outliers were removed based on an extreme mismatch between the test plan and the observations actually recorded. It is deemed that such a mismatch signals, with high probability, either poor familiarity with the sequential testing methodology or very poor execution, making statistics derived from these questionable. The removal of these outliers had the most material effect on the AGILE efficiency numbers presented with a positive impact of 3-4 p.p..
Additionally, 22 tests with estimated lifts of over 100% were removed as such results have a high probability of not being based on actual data of sound quality. After all three screens, the number of tests remaining is 1,001.
Given known characteristics of the majority of the users of Analytics Toolkit, the A/B tests are likely to be representative of those conducted by advanced and expert CRO practitioners, as well as those with an above average knowledge and understanding of statistics.
Basic test characteristics
The basic characteristics of the analyzed sample of A/B tests include the test duration, sample size, and the number of tested variants per test. Test duration provides information on the external validity of tests. Sample sizes provide an idea of the statistical power and quality of the estimates, whereas the number of variants is a simple gauge of how often practitioners test more than one variant versus a control in so-called A/B/N tests.
Test duration
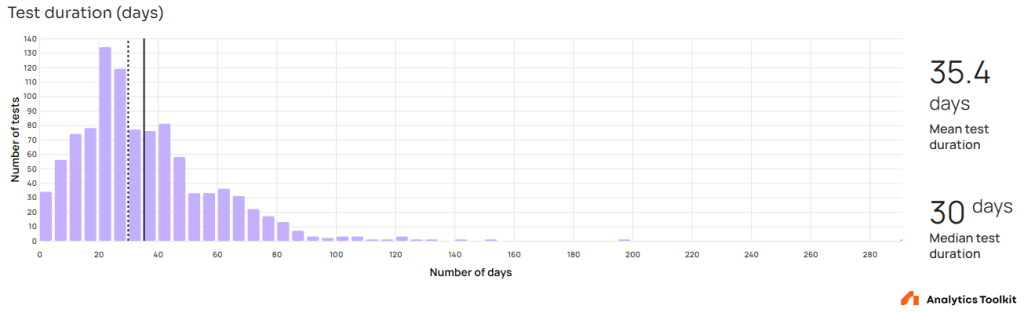
The arithmetic mean of all A/B test durations is 35.4 days which is equal to five weeks. The median is 30 days meaning that half of all tests lasted less than a month. The majority of tests spanned a timeframe which allows for good generalizability of any results.
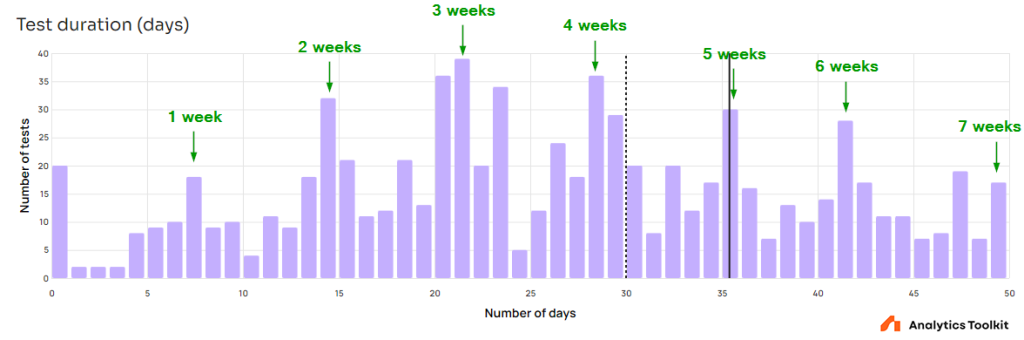
Zooming in the graph reveals notable spikes corresponding to tests monitored on whole week intervals: at 7 days (1 week), at 14 days (two weeks), at 21 days (three weeks), and so on until 49 days (7 weeks) at which point the pattern is no longer visible due to low amounts of data. It seems a significant number of tests are conducted by following best practices for external validity which should result in better generalizability of any outcomes.
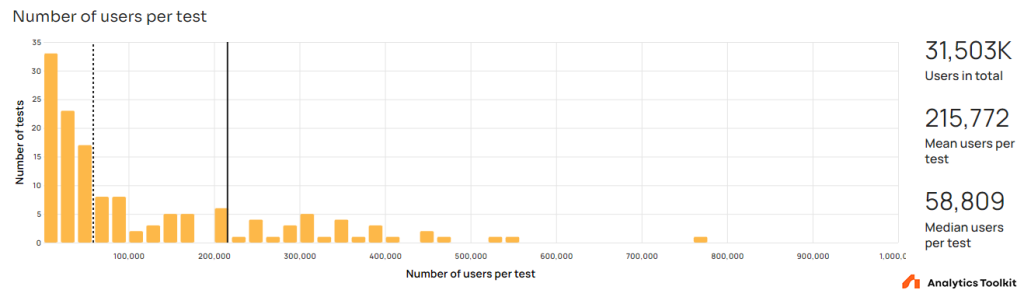
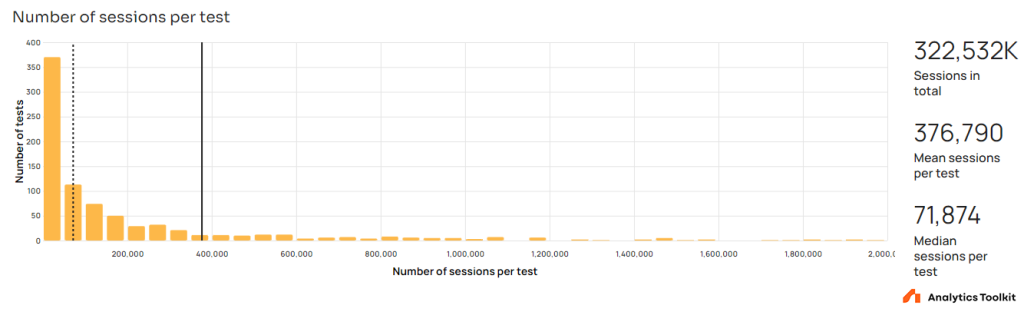
Sample size
For tests with a primary metric based on users, the average sample size is 217,066 users, but the median is just 60,342 users. For tests with a session-based metric the average sample size is 376,790 sessions while the median is at 72,322 sessions.
The power-law-like distribution is hardly surprising, given that a power-law distribution characterizes how users and engagement is split among web properties and mobile apps.
Sample size in itself has little to say without the context of baseline rates and standard deviations of the primary metrics, but we can safely say that the sampled tests include sufficient numbers of users or sessions to avoid statistical complications associated with very small sample sizes.
Number of variants
The vast majority of tests (88%) conducted on the Analytics Toolkit platform included just one test variant and a control. Only 10% included two variants, and just 2% included three or more variants. It seems most expert conversion rate optimizers prefer to plan tests with a single, well-thought out intervention, rather than to spend more time testing a more diverse set of ideas in a single go. One can speculate that this reflects a preference for incremental improvements implemented quickly versus more complicated tests that take longer, each carrying higher uncertainty.
Advanced test parameters
The advanced test parameters reflect key aspects of the all-important statistical design of the A/B tests in the dataset.
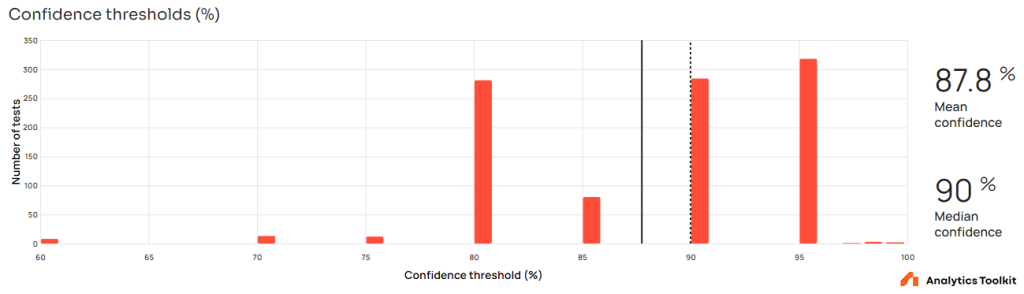
Confidence threshold
The distribution of confidence thresholds shows that in the majority of tests the threshold is between 80% and 95%, with a few exceptions below and above. The fact that the confidence threshold values are distributed somewhat evenly within this range is not at odds with a situation in which users are utilizing either the wizard or their own risk-reward calculations to arrive at a specific threshold matching the case at hand. The small number of thresholds higher than 95% likely correspond to tests with higher stakes in case of a wrong conclusion in favor of a variant.
This good practice can be contrasted to the one-size-fits-all approach of applying a 95% confidence threshold approach “by default”. The latter is typically suboptimal from a business perspective.
The confidence thresholds distribution seem to indicate an informed balancing of the two types of risk in A/B tests and can be viewed as a positive for the business utility of these tests. The data, however, cannot be conclusive in itself.
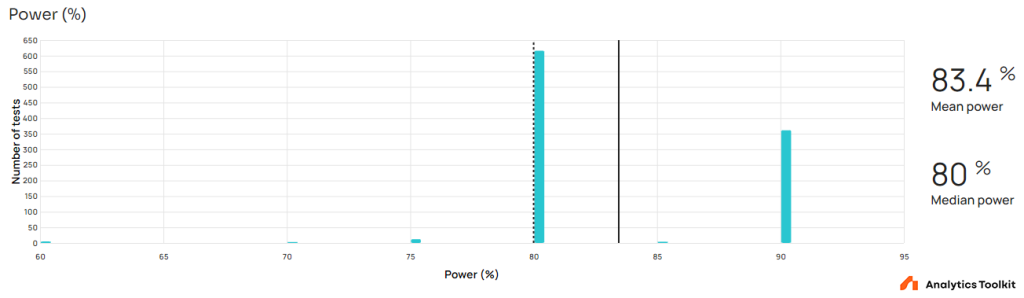
Statistical power
A significant majority of tests are powered at 80%, however a significant minority of roughly a third of tests are powered at 90%. This is encouraging since 80% power offers a fairly low chance of detection of a true effect of the target minimum effect of interest. It is better to explore the relationship of the minimum effect of interest and the minimum detectable effect at the 90% point of the power curve when planning tests.
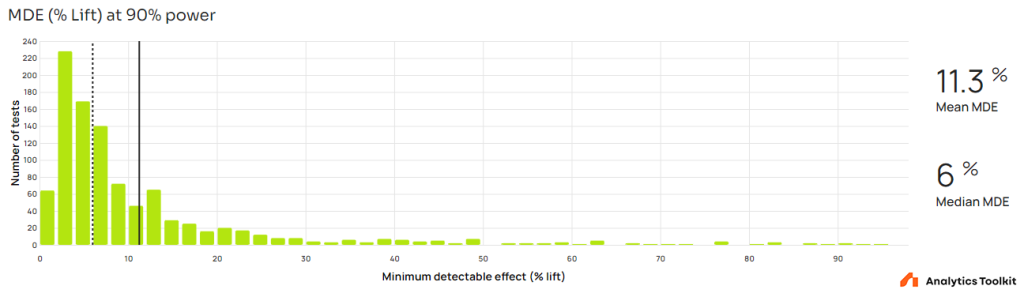
Minimum detectable effect (MDE)
The distribution of minimum detectable effects at 90% power is plotted below with a mean of 11.3% and a median of 6% lift.
Two thirds of all tests had a minimum detectable effect below 10% lift, which is significantly more than the roughly one quarter of tests with such parameters in the previous meta analysis [1]. The median of 6% means that half of tests had an MDE below 6% relative lift. It is probably an effect of both the guidance of the wizard and the experience of the practitioners using the tool. There is the obvious difficulty of untangling the two with just the data at hand.
The above numbers can be interpreted as tentatively supporting the conclusion that at least some of the unrealistic MDEs observed in the 2018 meta analysis [1] were linked to unaccounted peeking.
In any case, these are highly encouraging numbers, especially in light of findings in the following section.
Outcome statistics
Lift estimates are the simple unbiased maximum likelihood estimator for fixed-sample tests, and a bias-reduced maximum likelihood estimator for sequential tests.
Percentage of positive outcomes
About 33.5% of all A/B tests have a statistically significant outcome in which a variant outperformed the control. This is higher than the 27% observed in the previous meta analysis [1], and in the upper range of industry averages reported in an overview by Kohavi, Tang, and Xu (2020), page 112 [2]. Given that there is no outcome bias in the inclusion criteria for this meta analysis, this number can be viewed as evidence for the relatively higher quality of the tested ideas and their implementation (a.k.a. interventions).
This high proportion of ‘winners’ is not entirely surprising given the known profile of the users of Analytics Toolkit in which advanced and expert CRO practitioners are overrepresented. It shows the value of accumulated knowledge and experience and likely means that these professionals are better at filtering out poor ideas and/or is indicative of the sway they have over decision-makers regarding what ideas reach the testing phase.
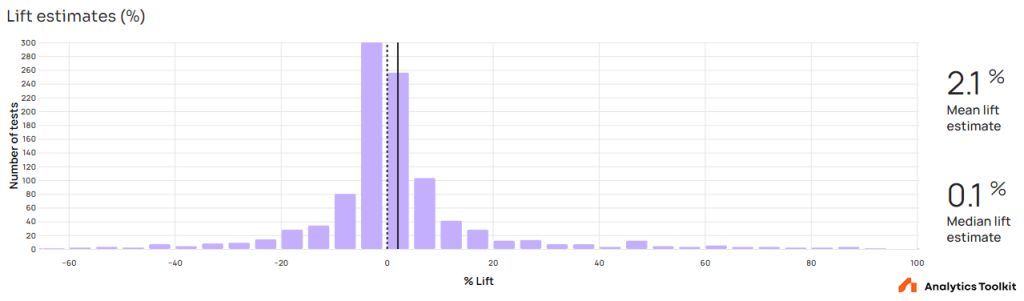
Lift estimates
Despite the optimistic number above, one way to interpret the lift estimates of all A/B tests conducted is as showing limited ability of this elite cohort of professionals to generate and implement ideas which bring significant value to an online business. The median lift estimate is just 0.08%, whereas the mean is 2.08% (standard error is 0.552%). This means that nearly half of the tested interventions have no impact or a negative impact. Even among the positive estimated lifts the majority are below 10%. On the flip side, the majority of negative estimated effects also have an impact of less than 10%.

(courtesy of GIGAcalculator.com)
The lift estimates are decidedly not normally distributed with a p-value < 0.0000001 on all five of the battery of tests supported by GIGAcalculator’s normality test calculator. The tails are quite heavy, with skewness towards the positive end. Estimates around zero are dominating the shape.
The above data reveals that affecting user behavior is hard either way. It is equally as difficult to influence a user to perform a desirable action as it is to sway them away from a goal they are intent on achieving. Nevertheless, the positive median and mean reflect that tested interventions have a better than coin flip probability of having a positive effect, with the difference from zero being statistically significant (p = 0.000084; H0: %lift ≤ 0) with the relevant 95% interval spanning [1.172%, +∞).
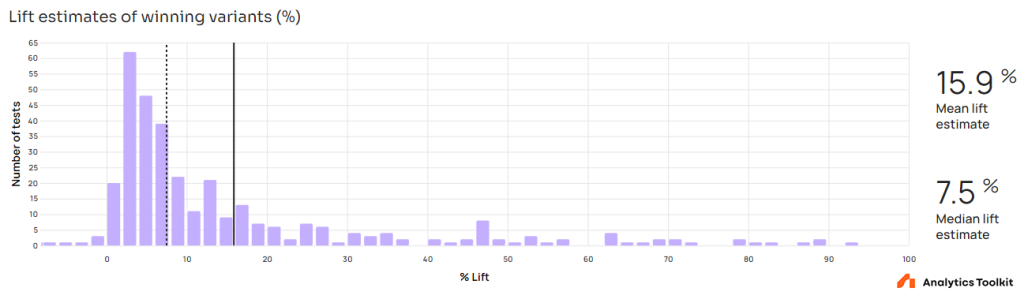
Of the statistically significant positive outcomes, the median lift estimate is a respectable 7.5% whereas the mean is a whopping 15.9%! The standard deviation is 19.76%, with confidence intervals for the mean as follows: 95%CI [13.76%, 17.98%]; one-sided 95%CI [14.1%, +∞). This means that tests with ‘winning’ variants are likely bringing significant value to the businesses.
In a few cases the lift estimates of winning variants are below zero, which reflects non-inferiority tests. Given that some of the positive estimates are also from non-inferiority tests the likely benefit of the above lifts may be even greater than the numbers show.
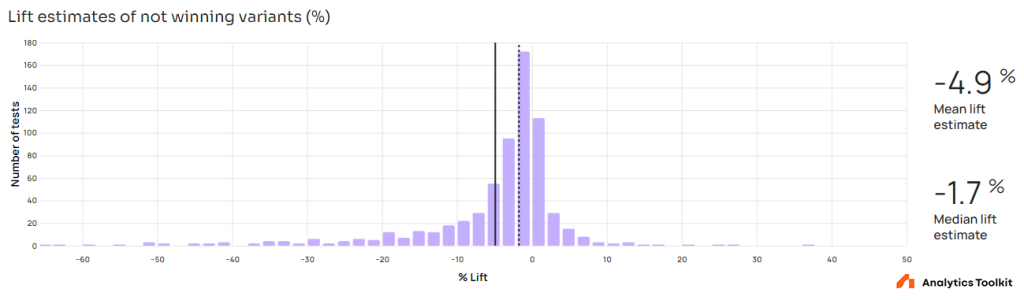
Of the tests which concluded without a statistically significant outcome most have a negative estimated lift, while some have positive estimated lift. With a mean of -4.9% and a median of -1.7% these demonstrate why it is so important to perform A/B tests (SD = 10.8%, 95%CI [-5.70%, -4.07%], one-sided 95%CI (-∞ , -4.201]). In many scenarios, it is unlikely to detect such small impacts in a non-experimental setting due to the much greater uncertainties involved in any kind of observational post-hoc assessment (change impact estimation).
Efficiency of sequential testing
The statistics in this section reflect various aspects of sequential testing and its performance. Sequential experiments are planned for a certain maximum target sample size and a number of interim evaluations to reach that target, but may stop (“early”) at any evaluation depending on the observed data up to that point. The efficiency of sequential tests depends both on the type of sequential testing performed, the testing plan, and the true effect size and direction of the tested intervention.
Average stopping stage
Sequentially evaluated online experiments using AGILE are planned for 10.8 monitoring stages on average. These tests have stopped on analysis number 5.6 on average, suggesting they stopped at half of their maximum planned test duration / sample size. This is in line with the expected performance of sequential testing, meaning that one can plan longer maximum run times for tests with peace of mind due to the expectation that they will terminate much earlier if the results are overly positive or overly negative relative to the minimum effect of interest.
Actual versus maximum running time
Both the stopping stage and the actual running time of a sequential A/B test depend on the true effect size and direction of the tested intervention. The distribution of actual running times as a percentage of their respective maximum running time is presented below.
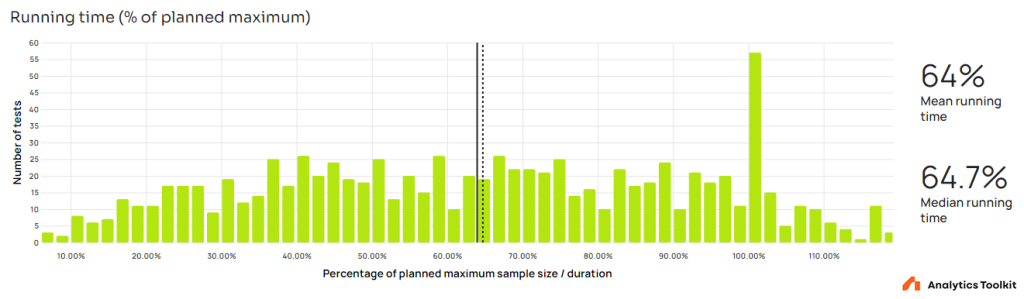
The mean and median are nearly identical at 64% and 64.7%, meaning that tests stopped, on average, at just under two thirds of their maximum planned run time.
There is a significant spike of 57 tests stopped at exactly 100% of their maximum running time which suggests either a higher than expected number of tests with just 2 monitoring stages and/or a number of tests planned to perfection (very stable rate of users or sessions per unit time), and/or tests entered post-factum for whatever reason. Two-stage tests are a small factor, but it is difficult to distinguish between the other two. It is therefore likely that these represent artificial tests (e.g. reanalyzing a test post-hoc for the purpose of comparing estimates with a fixed-sample analysis) instead of actual tests planned and analyzed using AGILE.
If this is assumed to be the case, then these tests are skewing the distribution upward and the true mean and median are instead at about 62% of the maximum running time, slightly improving performance. However, the probability that the majority of such tests are actually artificial is judged to be low enough to not warrant outright exclusion from the analysis.
Performance versus equivalent fixed-sample tests
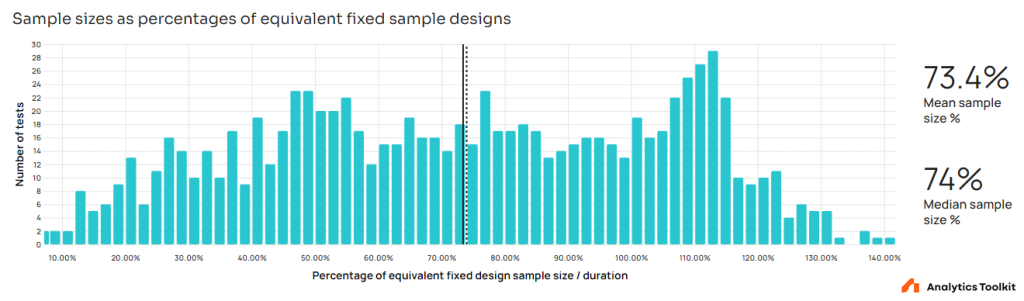
The performance versus fixed-sample equivalents mirrors that of the performance versus the maximum running time with a the spike appearing between 105% and 115% of fixed-sample equivalent since 5-15% is the expected worst-case sample size inflation in most tests between 5 and 12 analyses. The mean and median sample size of sequential tests is 73.4% and 74% of that of an equivalent fixed-sample test, respectively. This puts the average saving in both time and users exposed at around 26%. These numbers would improve to about 71.5% and about 28.5% if the unexpected spike between 105% and 115% is removed from the data.
To my knowledge, this is the first of its kind meta-analysis of the actual performance of a robust frequentist sequential testing method with real-life interventions in online A/B testing. It proves the benefits of using sequential testing over fixed-sample testing, although the impact is somewhat dampened versus estimates which is mostly explained by the distribution of the estimated lifts of all tests which is far from normal, with significant concentration of density around zero.
Takeaways
The meta-analysis achieves its first two goals by presenting an outcome-unbiased collection of nearly ten times more tests than a previous meta-analysis. It also provides provisional evidence of positive effects of using the Analytics Toolkit test planning and analysis wizard.
The evidence for the benefits of sequential testing in a real-world scenario is substantial and at minimum supports a 26% performance increase in terms of running time / sample size, with possible greater improvement in the ROI of testing due to the disproportionate sizes of the true effects in tests stopped early for either efficacy or futility.
The meta-analysis also produced the following key numbers:
- 33.5% of A/B tests resulted in a statistically significant positive outcome with a mean effect of 15.9% while half of them had an estimated effect of greater than 7.5%.
- The median lift of all tests is estimated at 0.08%, and the mean at 2.08%, demonstrating benefit of CRO expertise with a statistically significant difference from zero.
- For the majority of tests the estimated lifts are close to zero, which has significant consequences for power analysis and sample size planning. Importantly, it proves the need for randomized controlled testing with robust statistical estimation over observational methods which would have much poorer capabilities for detecting such minute changes.
- The benefit of sequential testing in real-world scenarios is at least 26% in terms of average efficiency improvement versus equivalent fixed-sample size tests
- 88% of tests are simple A/B tests, and only 12% are A/B/N, with the majority of them having just two variants versus a control, suggesting that expert CROs prefer to keep it simple and iterate rather than to run more complex tests.
- The typical test duration is about a month, or between four and five weeks, suggesting good generalizability of outcomes, on average.
- A/B tests include on average between 60,342 (median) and 217,066 (mean) users, and between 72,322 (median) and 376,790 (mean) sessions.
- Most online experiments are conducted with a confidence threshold between 80% and 95%.
- Half of A/B tests have 90% probability to detect a true effect of 6% or less, while the average MDE is 11.3%, suggesting a trend towards better-powered tests becoming the norm among top professionals.
Under the assumption that a majority of tests in the analysis were performed on key business metrics and few were on less sequential user actions, one can infer about the benefits of testing over implementing straight away. Of two identical companies wishing to implement identical changes, the one which implements only changes that pass an A/B test would achieve multiple times faster growth than the one which just implements everything. It would also grow much smoother which really matters in business. The advantage of the former would come from implementing only winning tests with a mean lift of 15.9% compared to a mean lift of just over 2% for the latter, despite winning tests resulting in implementing just over a third of all proposed changes.
While this last conclusion might be stretching it a little, it should be a prime example of the significant marginal benefits of testing when accounting for the statistical overhead. The various overheads of preparing, running, and analyzing tests need to be accounted for separately, with the typical economies of scale at play.
References:
1 Georgiev, G.Z. (2018) “Analysis of 115 A/B Tests: Average Lift is 4%, Most Lack Statistical Power” [online] at https://blog.analytics-toolkit.com/2018/analysis-of-115-a-b-tests-average-lift-statistical-power/
2 Kohavi, Tang, and Xu (2020) “Trustworthy Online Controlled Experiments: A Practical Guide
to A/B Testing”, Cambridge: Cambridge University Press. isbn: 978-1-108-72426-5. doi:
10.1017/9781108653985




Great work! Really interesting data. Could we get some more context on what types of AB tests were run? Were these primarily assessing the impact of marketing campaigns?
Thank you, Richie. We are mostly blind to the types of tests and other such context, but given the typical profile of our users, it is likely that most were CRO tests related to website or app changes.