Georgi GeorgievI see a nice trend in recent discussions on A/B testing: more and more people realize the need for proper statistical design and analysis which is a topic I hold dear as I’ve written dozens of articles and a few white-papers on. However, there are cases in which statistical validity is discussed without consideration for the generalizability of the results of A/B tests which leads to confusion and the adoption of poor practices. This is most pronounced in discussions on what sample size is appropriate, what methods for sequential testing with continuous monitoring of test results are appropriate, as well as whether one can accept the outcome of a test if it is highly statistically significant, but it has been obtained with a small sample size.
This post aims to bring some clarity on the difference between and statistical validity and external validity, to highlight common issues with generalizability of the results of A/B tests and to discuss ways to address them by requiring representative samples.
What is external validity / generalizability?
An accepted definition of external validity as applied to scientific experiments is supplied by Campbell & Stanley [1]:
“External validity asks the question of generalizability: To what populations, settings, treatment variables and measurement variables can this effect be generalized?”
Examples of issues of generalizability in science are the prolific testing on students and quasi-anonymous online collaborators in psychology (do students and mturks represent the broader population well-enough?) and the lack of test subjects of certain gender, ethnic, religious etc. groups in some clinical trials (do the treatments have the same main effects and side effects on them?). It is also a constant issue in political polls and other surveys, including consumer research. In A/B testing we do not have to deal with some of these issues due to the way the experiments are set up, but there is plenty else to worry about, as we shall see.
The external validity of an A/B test (a.k.a online controlled experiment) is defined by the applicability of its results for populations and times different than the ones examined during the test. Therefore, the larger the population to which the results are generalizable, the better, especially given that in practice we rarely even know what the full population is as we can only guess how external factors like marketing strategy, competitor actions, broad economy trends, tech trends, regulatory action, etc. will shape the future potential clients of an e-commerce store, for example.
Given this definition, it should be immediately clear that:
Obtaining accurate statistical estimates of the effect of the tested intervention during a test is important for managing business risk but the results will hardly be of value if they do not provide an accurate reflection of the true effect on future visitors to our site.
An A/B test may be demonstrating a strong positive effect with a very low p-value (high statistical significance) and a narrow confidence interval for relative lift, yet if it lacks external validity the business may fail to register any discernible gains or may in fact generate losses if the result in the general population is of the opposite sign. In other words, unless our results are generalizable to future potential clients any prediction we try to make about future sales, revenue, conversion rates, and so on will be inaccurate and may even be opposite to the true direction of the effect.
Threats to generalizability of A/B testing results
The main issue with factors that can affect the generalizability of an A/B test is that there are potentially infinitely many such factors, they are often impossible to predict and therefore to measure. Unlike physics experiments where one is fairly certain that the laws of nature will not change from one day to the next, these immeasurable risks are inherent to any prediction made for an open and changing environment such as consumer behavior.
Still, there are some known threats to generalizability which can be countered to an extent by acquiring more representative samples, given we are aware of them. I distinguish three broad categories of such factors:
- time-related factors
- population change factors
- novelty/learning factors
Examples of time-related factors that may result in time-variability of user behavior are: within-day differences (e.g. morning vs. evening), day-to-day differences, day of week differences, holidays versus workdays, seasonal effects. Some niches are more prone to these effects than others, for example the seasonal cycles in the tourism and travel industry are much more pronounced than the general food consumption industry (ice-cream, beer and many others being prominent niche exceptions). For example, people looking for a new TV alone during the day may have a different approach to shopping than those doing so as a couple in the evening (in this case time being a proxy measure for a third factor). People visiting your travel offers website on a Tuesday may be more likely to just browse while those visiting it on a Saturday may be more likely to actually complete a reservation or purchase. These are just a few basic examples of how the time-period analyzed during an A/B test may affect external validity when the results are generalized to a longer time period.
In addition to that we may have time-to-effect factors such that users who take action quickly after experiencing the intervention may behave differently than those who take more time to deliberate or consult third-parties. The differences might be in the size of the effect but also in its direction: something which works well for impulsive buyers may have the opposite effect on more deliberate customers thus negating or even reversing the effect entirely when the tested treatment is applied to the whole population over an extended period of time. A relatively quick experiment may fail to properly capture the behavior of the latter. Note that “quick” here might be hours, but it may also be weeks, depending on the typical purchase cycle of the product or service at hand. While seasonality is somewhat better understood, I’ve not seen many people mention considerations for time-to-effect factors.
Population change factors include any significant shifts in the composition of the population of interest either during the test or after it. For example, during a week-long A/B test a major competitor may launch a huge promotion the likes of which will not be seen for a year, or maybe several years. The outcome of your test may be invariant to that event, but it may also skew the results obtained during that week which coincided with the promotion in such a way that they become externally invalid and backfire when implemented permanently. An even more trivial example is that the test might coincide with a big advertising push from your marketing department or maybe there were atypical volumes of organic social media traffic. In yet another scenario your primary source of traffic is the U.S. but for some reason during the test you get an unusually high amount of traffic from the U.K. and Australia which subsides afterwards. If the population change was a factor in the test outcome, once the event is over this factor is no longer present and the test’s predictive capacity is destroyed or hindered.
Novelty and learning factors can be a significant issue when you have a solid base of returning users which is especially true for big e-commerce websites, but can apply to small niche sites with a loyal customer base as well. A novelty effect is a positive or negative initial reaction to a change, which is dampened at some rate over time. A typical example is how when doing a major redesign of a process users are often a bit lost in their first few interactions with the new flow, resulting in worse KPIs. After a while they get used to the experience and the KPI recovers to previous levels. On the contrary, introducing an attention-drawing change might trigger an initial spike in the KPI, but after getting used to it users stop responding to it as much and things return to baseline (some call this regression to the mean, which I find to be incorrect as regression to the mean is a very complex phenomena with many explanations which can be true separately or at the same time).
Such novelty effects are often called “learning effects”, as they usually involve some form of increasing familiarity leading to a corresponding increase or decrease of a KPI.
The above mostly relates to conversion rate optimization (CRO) as applied to websites, but the same principle applies to other forms of A/B tests such as in email marketing. While email marketing is in a slightly favorable position since the people in our email list do not change on a daily basis as it happens with the general audience of a website, it is by no means immune from threats to external validity. In A/B tests in mail marketing generalizability is threatened in similar ways: the email list may grow from traffic sources vastly different from the ones that brought in the subjects we tested on; if the test was a single email burst unique one-time events might have been in play which might have skewed the results; external factors may change; etc.
All of the above examples may or may not lead to externally invalid outcomes in both directions. They may suppress the discovery of a genuine beneficial effect or they might make it appear as if there is an effect when in fact these results only apply to an atypical set of users exposed to the test and not to your typical users. No matter how good your statistical design and estimation is it will not protect you from these effects unless you try to mitigate them through a proper design of the A/B test. This is true even for the smallest p-values and highest levels of confidence you can observe and even if a confidence interval shows a large probable lift.
Improving generalizability of A/B tests
No matter how daunting all three types of threats to external validity may seem, there is one solution which addresses, to an extent, all of them at the same time: longer duration of the test and consequently a larger sample size. I think in an A/B testing environment this is the single biggest factor in improving the representativeness of the sample and testing with a more representative sample means greater generalizability of the results.
Time factors that depend on some kind of seasonality are dampened the longer the test runs. The effect of any intraday variability is normalized when you sample over several days. Similarly, the effect of any day-of-week variability is normalized when you sample a whole week or even better: several full weeks. Any time-to-effect factor is also partially accounted for once you sample long enough to cover at least one full buying cycle. This is the reason why our A/B test ROI calculator suggests weeks as the base time unit in which to plan a test, encouraging you to plan for 1,2,3… weeks and not for 10,15,20… days.
Short-term population change factors should also play less of a role the longer the test runs for. However, no matter how long you run the test for, if a significant shift in the qualities of the population occurs after the test is completed, external validity will suffer no matter what.
Similarly, novelty/learning effects are given more time to become pronounced with a longer test duration which should translate in better overall generalizability. In 2015 several Google employees published a very interesting paper [2] proposing a method for estimating long-term learning effects from short-term tests, but it is far from trivial to implement, it is limited in terms of applicable scenarios and will likely be unable to capture learning effects with delayed onset. If you do not have the technical resources to implement a similar solution, your best bet remains to allow for longer testing times.
Sequential monitoring of test results and representative samples
The above threats to generalizability and solutions for obtaining representative samples are even more important in a test in which instead of evaluating the data once at the end (fixed-sample tests) we monitor the data as it gathers and have the opportunity to make the decision to stop the test at any of these evaluation times. I am obviously not referring to the malpractice of peeking at the data while “waiting for significance” or its equivalence with a Bayesian approach which would be similarly affected. I am referring to proper sequential testing procedures such as AGILE A/B testing.
The issue with sequential evaluation of an A/B test is that one can get a very good or a very bad statistically significant result very early into the test. Assuming that the significance threshold was chosen following a well thought-out risk-reward calculation should one stop the test early due to efficacy or futility, while risking the generalizability of the result?
My answer would be “no” and “yes”. It will be “no” if a simple version of Wald’s Sequential-Probability Ratio Test (SPRT) or an equivalent procedure was used. SPRT and SPRT-equivalent methods have been proposed by some statisticians and some are, as far as I know, implemented by vendors of A/B testing software. The reason I’m recommending against their adoption is that they allow one to stop too early way too often with results which are not impressive enough (extreme enough) to justify the potential loss of generalizability.
My answer would be “yes” if a different approach is used in which an alpha-spending function is constructed such that alpha is spent conservatively early on and more aggressively later on thus seeking a balance between fast decision making and better external validity (by way of obtaining a more representative sample):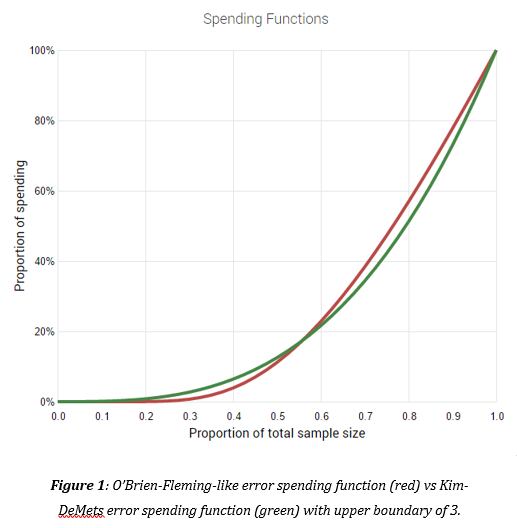
This is a quote for the justification of the choice of spending function from my 2017 paper [3]:”The method used by default for the construction of the efficacy boundary in our AGILE AB testing tool is a Kim & DeMets (1987) power function with an upper boundary of 3. The choice is justified by the fact that the function is a bit less conservative than the O’Brien-Fleming-like spending function in the early stages of a test, but is still conservative enough so that more error is allocated to the later stages of a test. Here by conservative it is meant that initial results must be very extreme before an early conclusion would be suggested – which is a good property as early users in a test are not always representative of later ones.”. This article, in fact, provides an extended argument in support of this choice.
The above-mentioned alpha spending method is used by all users of our AGILE A/B testing statistical calculator.
In conclusion
While it is of crucial importance that A/B tests are preformed using good statistical methods for estimating effect sizes and related margins of error it is equally important to design online controlled experiments which address the need for generalizability of the results to future populations. Having a statistically rigorous test is a necessary requirement, but it may be insufficient or even backfire unless it is acquired using a reasonably representative sample.
The three major threats to generalizability in A/B testing are time-related factors, population change factors, and learning effects (novelty effects). While we can never eliminate these threats, we can achieve better external validity by increasing the time duration of A/B tests so that they take into account known purchase cycles and seasonal cycles, reduce the likelihood of one-time events affecting the structure of the population, and allow for learning effects to manifest at least partially. The need for acquiring a representative sample should be taken into account when applying sequential testing procedures so that they offer a good compromise between speed of testing and generalizability of the observed results.
References
1 Campbell D.T., Stanley J.C. (1966) “Experimental and Quasi-Experimental Designs for Research”, Rand McNally.
2 Hohnhold H., OBrien D., Tang D. (2015) “Focusing on the Long-term – it’s Good for Users and Business”, Google
3 Georgiev G.Z. (2017) “Efficient A/B Testing in Conversion Rate Optimization: The AGILE Statistical Method”, Analytics-Toolkit.com
About the author
Managing owner of Web Focus and creator of Analytics-toolkit.com, Georgi has over eighteen years of experience in online marketing, web analytics, statistics, and design of business experiments for hundreds of websites.
He is the author of the book "Statistical Methods in Online A/B Testing" and white papers on statistical analysis of A/B tests, as well as a lecturer on dozens of conferences, seminars, and courses, including as a Google Regional Trainer.
