Multivariate Testing – Best Practices & Tools for MVT (A/B/n) Tests

Let’s get this out of the way from the very beginning: most “A/B tests” are in fact multivariate (MVT) tests, a.k.a. A/B/n tests. That is, most of the time when you read about “A/B testing” the term also encompasses multivariate testing. The only reason to specifically differentiate between A/B and MVT is when someone wants to stress on issues or concerns specific to running more than one variant against a control. Which is, in fact the only thing by which A/B/n tests differ from A/B tests – there is more than one variant tested.

So, given that running an MVT scenario is pretty much the same as running a basic A/B test, the relevant question is why aren’t all split tests multivariate and why don’t we just test every possible combination of changes we can think of, at the same time. Below I’ll answer these questions, explain the specific challenges that arise in planning, executing and doing statistical analyses of such tests, and recommend some good practices that you can follow as a CRO or UX specialist.

But, first:

What is multivariate testing?

There are common misconceptions about what MVT is, so we need to get the meaning of the term right, before we proceed any further.

Some sources, including a ConversionXL article and a Wikipedia article, incorrectly state that:

“Essentially, it can be described as running multiple A/B/n tests on the same page, at the same time.”

(CXL, in “When To Do Multivariate Tests Instead of A/B/n Tests”)

“It can be thought of in simple terms as numerous A/B tests performed on one page at the same time.”

(Wikipedia, in “Multivariate testing in online marketing”)

The statements are practically identical and describe running concurrent A/B or A/B/n tests. This is not the same as multivariate testing. Concurrent testing can lead to certain complications, as you can read in Running Multiple Concurrent A/B Tests: Do’s and Dont’s .

Other sources, like Oracle’s page on the topic, write:

“Where AB or A/B Testing will test different content for one visual element on a page, multivariate testing will test different content for many elements across one or more pages to identify the combination of changes that yields the highest conversion rate.”

First, we have an incorrect definition of what A/B testing is – there is no limit on how many visual elements on a page you can change in an A/B test. Second, we have a definition of multivariate testing that can be understood as both concurrent A/B testing and as a true multivariate (A/B/n) test, depending on the particular case at hand. In fact, the definition given for multivariate doesn’t really add anything to the definition of an A/B test.

So, just so I’m sure we’re on the same page, here is the definition I believe most correctly captures what a multivariate test is:

A multivariate test is the same as an A/B test, but with more than one variant tested against a control.

Like a strict A/B test, an A/B/n test is an online controlled experiment which uses randomization to spread uncontrolled variance to a set of interventions, each of which is compared to a control. It allows conversion optimization experts to establish causality between what they are doing to improve the UX or conversion rate and the observed outcomes. It is also what makes it possible to predict, with a known uncertainty, how the improvements observed during the testing period will hold in the future.

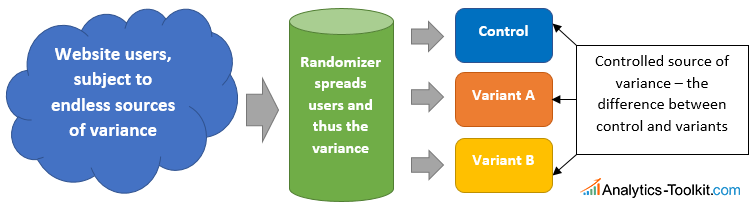
Benefits and drawbacks of using MVT

Or in other words, when to do a multivariate test, instead of a simple A/B test? The obvious drawbacks are the increased complexity to design, develop, QA and deliver such tests, as well as the increased complexity of the statistical analysis – basic statistical significance tests such as chi-square, t-test, z-test, etc. can no longer be applied as easily.

While reviewing posts on the topic for situations where MVTs are beneficial, I saw three common recommendations. One is to always run multivariate, instead of A/B tests. The justification being that they are more efficient. The second common recommendation is to run A/B tests for big changes that can possibly result in big improvements, while multivariate is more suitable for smaller changes and improvements.  The third is to run multivariate tests when it is not enough to know that a set of changes work better than the control, but it is important to know how much each change contributed to the improvement (most often a lift in conversion rate). Let’s examine each one in detail.

1.) Are multivariate tests more efficient than A/B tests?

If we use a definition which incorrectly equates multivariate testing to concurrent testing, then running many tests on the same population at the same time achieves superior efficiency than running A/B tests on the same exact things one after another. The trade-off is that it can lead to wrong conclusions, especially if fully automated testing is used where interference between the tests can remain undetected (more here). These issues can be alleviated by a manual review of the interaction between the tests and/or post-test segmentation of the results to identify strong opposing effects for certain variations combinations.

Using the correct definition of “multivariate test = A/B/n test”, the efficiency improvement question becomes a bit more complicated. The reason is that each variant you want to test increases the sample size requirements (and as consequence – the time requirements) of the test. The reason is that when comparing many variants to one control, the likelihood of committing a type I error and wrongly declaring a “statistically significant” winning variant increases. Sample size adjustments are needed in order to achieve the same level of statistical guarantees. I examine the question in a bit more detail in point #4.5 of the white paper “Efficient A/B Testing in Conversion Rate Optimization: The AGILE Statistical Method” (free download).

Here are some calculations performed with the AGILE A/B Testing Calculator for the number of users that you would need to commit per variant and for the test as a whole:

# of Variants Tested	Sample Size per Variant	Total Sample Size	Sample Size per Variant – % of A/B test	Total Sample Size – % of A/B test
1	9,735	19,470	–	–
2	8,620	25,860	-11.45%	+32.82%
3	8,163	32,652	-16.15%	+67.70%
4	7,885	39.425	-19.00%	+102.49%
5	7,723	46,338	-20.67%	+138.00%

 

You can easily see that increase the number of tested variants from 1 (A/B test) to 2 (A/B/C test) increases the total required sample size by ~33%. Running two consecutive tests: A/B and then winner of A/B vs C would likely take 2x more users, or +100%, so +33% is still an improvement, but it is obvious that testing more comes with a cost in this case.

In both scenarios above there is a hidden assumption about the tested variants, without which the efficiency gains disappear and turn into drawbacks. That assumption is, in the concurrent testing case, that all A/B tests are created equal, and in the true multivariate case – that all variants we come up with have an equal chance of lifting the conversion rate or whatever dependent variable we are working to improve. These, of course, are simply not true in most cases.

Are all tests created equal?

Imagine this: instead of doing 10 changes to a page and running an A/B test, you split it into 10 A/B separate tests that run concurrently (this is going with the CXL/Wikipedia definition). If the original A/B test had a given statistical significance, power and minimum detectable effect (all necessary variables to run a proper statistical test – more on how to select these variables and the trade-offs involved), would you set the same parameters for the concurrent tests? If you do, then you gain no efficiency from splitting an A/B test into a set of concurrent A/B tests. Efficiency would only be gained if the concurrent tests could not be run as a single A/B test for technical or timeline reasons.

Furthermore, it doesn’t really make sense to use the same parameters for each of the smaller tests, since each change will be subtler and thus the sensitivity of the test would need to be increased, most often by increasing the minimum detectable effect. This leads to significant increases in the time required to run the test and can eliminate a lot of the efficiency gains obtained from splitting the test. So, a most natural thing occurs: as you desire to get insight into subtler things, the cost for each insight increases.

Do all variants have an equal chance to result in improvement?

If you have spent months researching roadblocks, issues and pain points that users have with a process and you designed a test version based on that, do you think it will have more, or less likelihood of beating a randomly generated variant which was produced by changing a few colors, and a few words here and there? I thought so. So, testing more variants for the sake of it results in a significant increase the sample size (and time) required to run the test, with little chance to achieve an improvement. So:

MVT is always more efficient compared to an equivalent sequence of A/B tests, but running a multivariate test is more efficient than testing just one variant only when the additional variants have a high likelihood to beat the control and a decent likelihood to beat the first variant.

The above, of course, assumes that most of the utility of running a test is in increasing the conversion rate and that the implementation and operational costs of the tested variants are roughly the same. In case there are considerations outside of these, a multivariate test may be justified even if it means testing longer.

Still, in most cases, it is advised to avoid running more variants “just because you can” due to the associated efficiency cost. Do so only when you have informed belief that there is a good chance that the cost will be justified. Don’t add a Variant C to an A/B test just to test if one shade of orange on the CTA button works better than another one. Don’t forget that cost to developing and QA-ing additional variants also has a negative impact on the ROI of running multivariate tests.

A side note: I believe the reason why the myth that running multivariate tests in UX and CRO is always better than running simple A/B tests, no matter which interpretation of multivariate you take, is the lack of adjustment of the statistics when such tests are done in practice. The increased Family-Wise Error Rate (FWER) means that tests will yield nominally statistically significant results, making for happy experts and customers in the short term, but poor actual results. If the test statistics are properly adjusted to account for the increase in, the results will be closer to the truth and the efficiency “gains” will be revealed for what they most often are – chimeras.

2.) A/B tests for big gains, multivariate for small changes?

I believe I’ve already addressed if multivariate is more efficient for small changes than a proper A/B test in point 1.) above, and have done so for both interpretations of multivariate testing (concurrent and the correct A/B/n meaning). If the test statistics are properly adjusted to account for the increase in type I errors, then there are efficiency gains only if the variants added to the A/B test are likely to result in an improvement versus the control. I see no argument based on the size of expected changes alone, that would make me chose a multivariate test over an A/B test, or a set of concurrent A/B tests over a single A/B test, where the variant combines the best combination of the small changes (chosen based on data + expertise).

3.) Are multivariate tests necessary to determine the effect of individual changes?

The answer to a straightforward question like this one is a resounding “yes”, no matter if you interpret “MVT” to mean concurrent tests, or if you take it for what it actually means: an A/B/n test. There is no good way to separate the effect of a particular change, when it is one among many in a winning variation.

However, the question here is: is this information valuable and what is the cost for getting it?

If you test the changes in isolation, as in each variant having just one change applied, and none of the others, you will miss likely interaction effects (both positive and negative) wherein the sum of the parts can and often does lead to a much higher difference in performance than the sum of the individual contribution of each change. So, not only will you need to test longer to detect smaller effects, you will not test the joint effect the whole set of changes, which might be very different from the results of the individual tests.

On the other extreme is testing each combination of changes against the control with no changes, sometimes called a full factorial test. Combinatorial explosion will quickly increase the number of variants to test, and, consequently, the time it would take to test them. Are you ready to commit that much time testing, not to mention issues with QA, deployment and monitoring, and analysis, just to know exactly which of the random combinations is the best and what the exact contribution of each factor is?

A middle-ground solution is to test only some of the many possible combinations against the control, which is often done when there is strong belief that several significantly differing combinations have a good shot at resulting in an improvement. This is what happens most of the time, but this is not detecting the effect of individual changes any more…

When to use multivariate testing?

In UX testing and conversion rate optimization, we want as much information, as possible. However, everything has a cost and it is proportional to the amount of detail we want to look at and the level of certainty we want to have about what we observe. That’s why deciding to add a variant to an A/B test, making it a multivariate A/B/n test, should not be made lightly.

If the information that can be gained from adding the variant is significant enough to justify the added complexity and sample size requirements, then by all means, do it, no matter how small or large the change is compared to the initial variant. If there is a good chance that a variant which is significantly different than the initial one will perform better than the control and hopefully better than the other tested variants, run a multivariate experiment.

In all other cases, I would advise you to retain from going MVT. Testing for the sake of testing was never a good investment of one’s time and resources…

See this in action

Try itA/B Testing Calculator
Advanced significance & confidence interval calculator.

Software tools that support A/B/n tests

Most, if not all major providers in the A/B testing industry support MVT designs, meaning that you can design multiple variants, run them at the same time and see the results. I won’t be providing a comprehensive list, as one can easily use Google to find the established players. The statistical analysis of the tests, however, can be a different story. I would suggest that you read the help section of the tool you are using or looking to use to see how they handle multivariate statistics – what methods are used to adjust for the increased error rate, what assumptions the method has, etc. If information is not available, ask away, see what they tell you about it.

As mentioned already, the rationale behind the approach used in our own A/B Testing Calculator is explained in a free white paper you can download from our site. Since it is compatible with most software that handles design and delivery of A/B tests, you can just use it in conjunction with these tools to handle the statistical analysis for you.

If you have questions or comments on what we covered here, post a comment below or on engage me on our social channels!

P.S. I didn’t at all intend this article to be a debunking type one, but that’s what it partially turned into, once I’ve glanced at what others before me have written on the topic. Sorry if you were looking for a more straightforward and simple explanation about multivariate testing.

About the author