In recent years a lot more CRO & A/B testing practitioners have started paying more attention to the statistical power of their online experiments, at least based on my observations. While this a positive development for which I hope I had contributed somewhat, it comes with the inevitable confusions and misunderstandings surrounding a complex concept such as statistical power. Some of them appear to be so common that they can be termed ‘myths’.
Here we’ll dispel three of the most common myths and I will also offer a brief advice on how to avoid all confusions related to the power of an A/B test. However, I will not discuss what statistical power is and how to compute it. For those unfamiliar with the concept I strongly recommend reading this brief entry on statistical power in our glossary of A/B testing terms before you proceed with the article. Owners of ‘Statistical Methods in Online A/B Testing’ might want to refresh their knowledge by reading Chapter 4: ‘Statistical Power and Sample Size Calculations’.
What is an Underpowered Test?
First, let us try to set our definitions straight. This will be helpful in our discussion further on.
An underpowered test is a statistical test which doesn’t have the necessary statistical power. Since power is the inverse of the type II error rate, an A/B test with lower than necessary statistical power has a higher than the acceptable type II error rate. This can also be expressed in terms of sample size – an underpowered test has a smaller than necessary sample size (e.g. number of users).
However, one should ask how we are to determine what the necessary statistical power of a test is. How to say what is an acceptable threshold for the type II error? What is the necessary sample size?
An easy answer can be provided in this manner: given a certain significance level, minimum effect size of interest (MEI), and sample size, an underpowered test is one where the sample size in question is not large enough for the test to reach its target power (e.g. 80%, 90%, type II error rate of 20% and 10% respectively). While being easy, it is still unsatisfactory since we have just introduced another unknown – target power. While it is common for tests to have a target power of 80% or sometimes 90%, a convention is by itself not a good justification for using any of these numbers.
A more complicated answer would involve a proper risk-reward analysis which will result in an optimal balance of type I and type II errors by taking into account a variety of considerations specific to the test at hand. The output of such an analysis will determine the optimal significance threshold, sample size, and respectively MEI at any given power level. If the MEI is chosen in advance instead, then the statistical power of the A/B test is a single number which we can call target power. It is by this target power that we can judge a test to be underpowered or overpowered.
So, after determining the target power, we would end up with an underpowered test if we decrease the sample size without changing any of the other parameters. If the target power of 90% would be achieved with a sample size of 200,000 users per test group, and we decrease the sample size to 180,000 users per test group, then that will make the A/B test underpowered relative to the target statistical power of 90%.
An underpowered test would have insufficient sensitivity to reliably detect the minimum effect of interest, if it truly existed. Reliability in the above scenario refers to having a high enough probability of correctly inferring an effect of a given size if it exists (hypothetical true effect).
We can see that making sure our test is not underpowered is important as otherwise we could end up with a higher than acceptable false negative rate. This means we would fail to pick up on true effects of a size which makes them interesting at an unacceptable rate.
This is especially concerning for CRO agencies and CRO/UX consultants as an underpowered test means that their efforts, even if fruitful to a certain extent, might remain unacknowledged. It is also concerning for businesses who after having invested significant resources in developing and testing a given solution might fail to rule out that it is not harmful simply by way of not having a statistical test with a sufficiently large sample size (see The importance of statistical power in online A/B testing for more on this).
It is no wonder then, that many consultants and in-house experts have started paying attention to the power of their tests. This, however, leads to several myths, three of which are examined below.
Myth #1: A Statistically Significant Test Should Also Have Sufficient Power to Detect the Observed Effect Size
Quite a mouthful, but this is an accurate description of a practice which I’ve seen on multiple occasions, including in answers to a recent informal survey among CROs on certain poor visualizations of statistical results.
Putting this myth to practice looks something like the following:
- Design and run an A/B test (a fixed-sample size one for simplicity);
- Gather the data and run the results through a significance calculator;
- Upon observing a statistically significant result, check if the test had sufficient statistical power to detect an effect size as large as the observed one;
In other words, it is not sufficient for the test to be significant in order to conclude in favor of the variant, it needs to also have sufficient power versus the observed effect size.
For example, take a test with the following design parameters:
- significance threshold – 0.01 (confidence level – 99%)
- minimum effect of interest – 5.0% relative lift
- target statistical power – 90%
- sample size – 1,053,114 users (total)
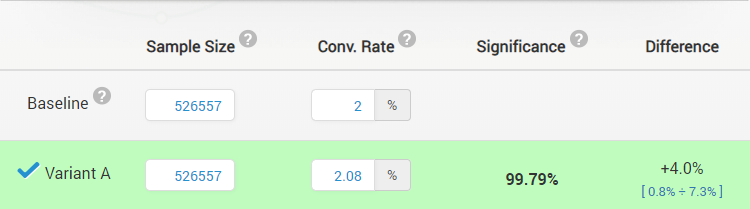
Upon observing the following outcome:
which has a p-value of 0.0021 (< 0.01) and a confidence level of 99.79% (> 99%) it will be noted that the sample size of 1,053,114 users provides only ~72% statistical power versus the observed lift of 4.0% and hence the test will be declared inconclusive (or perhaps worse, extended multiple times until it satisfies the power condition as well as the significance one, resulting in peeking with intent to stop).
Why is This Post Hoc Power Logic Wrong?
Simply put, if an A/B test results in a statistically significant outcome, we know we can reject the null hypothesis and continue by implementing the winning variant. Statistical power controls the type II error and since we are not in a position to make a type II error (which is to declare we failed to reject the null) it simply makes no sense to include the power of the test in determining whether to implement the variant or not. Given the inference we are going to make based on the significance level, the type I error control is all we should be interested in.
Furthermore, post hoc power calculations like these make precious little sense in themselves. A power calculation does not make use of any test data so computing it after the fact is the same as computing it before the fact.
Furthermore, if the power function is computed for the observed effect size, it becomes a simple transformation of the p-value and therefore adds no information that is not already contained in it. I can immediately tell you that any test which is barely significant at your target significance threshold will also have ~50% power for the observed effect size.
Mistaking the hypothetical actual effect sizes under which a power function is computed for the observed effect size from a given test is a major problem. Any given observed effect size can come from a range of actual effect sizes and there is no way to say which one it came from (that is why we have confidence intervals, for example, and point estimates, but we never say ‘the true value is the observed value’).
A power calculation only works with hypothetical effect sizes and says nothing about the expected observed effect size. An A/B test with 80% power against a 5% true lift has 80% probability of resulting in a statistically significant outcome. The observed value might be 3.5%, 4%, 5%, 5.5%, 6%, 7%, even 10% and the test may still end up being statistically significant.
I think the illogical nature of this statistical power myth can also be illustrated through a lottery example, albeit imperfectly. If one is happy to deny a statistical test its rightful conclusion due to it having low power, then one should also deny a lottery winner from collecting their winnings on the basis of their low probability of winning in the first place (before the draw). Saying ‘this test has low (whatever %) power to detect this observed effect size so the result is not conclusive’ is the same as saying ‘you had 1 in 100,000,000 probability to win the jackpot, so you’ve most likely cheated and I therefore will not pay up’.
Effect of Underpowered Test Myth #1
If the erroneous logic from Myth #1 of requiring that the A/B test is ‘powered’ for the observed effect size is followed, it leads to overly conservative tests with much larger type I error than planned, and a much smaller type II error.
Using the example above to illustrate: if we need to satisfy both conditions, then the observed effect size can’t really be smaller than the minimum effect of interest the test was planned for. The observed effect size must be 5% or larger before we would accept the test. The upper limit on the type I error of such a test is 0.0002 (much lower than 0.01) which corresponds to a confidence level of 99.98%, which is much higher than the target 99%. In fact this logic results in a 50 times more conservative type I error rate limit than what the test was planned for.
While there is nothing wrong in demanding more stringent type I error control, it should be imposed via the significance threshold and not via such an illogical usage of post hoc power.
In the case where this myth is combined with peeking, there is a certain mitigation of this effect due to the increase of the type I error from the peeking itself, but estimating the exact effect depends on too many random variables to be worth for the purpose of this short article.
Myth #2: The Observed Effect has to be Larger Than the Minimum Detectable Effect
We have already touched on how myth #1 logically leads to requiring us to effectively reject any true effect which leads to an observed effect smaller than the hypothetical effect of interest the statistical test was planned for.
Such a testing logic leads to another variant of the same mistake which is different only in how it is phrased. It is exactly the same in its essence, even though this might not be explicitly stated.
Using the example above, myth #2 would be to argue that since the observed lift of 4.0% is lower than the minimum effect of interest the test was planned for (5.0%), we cannot accept the result of the A/B test, even if statistically significant.
Using this logic one would not admit the variant to be a winner, even though the test is statistically significant simply because the observed effect size is smaller than the one we powered the test under.
In some sense this is arguably an even worse mistake than that of myth #1 since adhering to this rule means that even with infinite sample size and a confidence interval collapsing into a single point at 4.0% one would still not be permitted to claim that there is a positive lift simply because the observed effect being lower than the minimum detectable effect. That is, of course, if we somehow end up with a larger than the intended sample size in the test and that we don’t rerun the power calculations with the actual sample size but stick with the minimum reliably detectable effect chosen beforehand. Otherwise its consequences are precisely the same as myth #1.
I will not dwell more on this myth but I’d like to add that it stems from failure to distinguish between the actual effect size, the observed effect size, and the hypothetical effect size(s) under which statistical power is computed. The logic of why it is wrong and the effects stemming from that are pretty much the same as myth #1.
Myth #3 An Outsider Can Easily Tell If a Test is Underpowered
This myth mostly comes up as result of the first two myths about statistical power in combination with using conventions to design statistical tests. A lot of people will be tempted to assess the power of a test for the purpose of using it as part of myth #1 or #2. What is done is to simply take the sample size and run it through an effect size and power calculator using 0.05 significance threshold and 80% power.
What is wrong with that? As mentioned above, a proper risk-reward analysis is the only way to inform an adequate statistical design, including its statistical power versus a specified minimum effect of interest. Such an analysis features a dozen or so business parameters, each of which is often a combination of several numbers, many of which estimates themselves. Unless you are privy to these many numbers used, you are unlikely to know if a given sample size makes a test properly powered or not.
That said, there is another feature of a well-powered test and it is that it has a high probability of detecting effects in the range of plausible effect sizes. Still, it is not a judgement to be made lightly. For example, you can note how deliberate I am in classifying certain tests as underpowered in this meta analysis of 115 A/B tests where I base my judgement solely on the plausibility of the effect size each test has reasonable power against. I do not rule out alternative explanations for the observed sample sizes and hence power functions and I make this uncertainty very clear.
I urge for similar caution when trying to estimate whether a test is underpowered or overpowered as an outsider who knows little to none about what has informed the test. The only valid line of argument you can make in such a scenario is through the a priori plausible effect size range, which is, to an extent, subjective.
Closing Thoughts on Myths About Underpowered Tests
I hope this brief discussion is useful to anyone concerned about underpowered tests. I also hope you don’t feel tricked by the fact that the first two myths weren’t really about underpowered A/B tests, but rather about a peculiar error in how statistical power is applied post hoc. Since both myths are widespread exactly due to concerns about underpowered tests, I do believe they rightfully belong under this title.
I do think the issue, especially as defined in Myth #2, stems from the poor wording of the term ‘Minimum Detectable Effect’ (MDE) and I’ve made an extended argument in favor of the more accurate ‘Minimum Reliably Detectable Effect’ (MRDE) or the more intuitive ‘Minimum Effect of Interest’ (MEI). If you’re interested in learning more about this, Chapter 4.4 of ‘Statistical Methods in Online A/B Testing’ contains all you need to know.
All things considered, I believe minding the difference between hypothetical effect size, actual effect size, and observed effect size is crucial to blocking most misunderstandings about statistical power. The rest can be addressed by viewing power as a function and understanding how its three parameters influence its output.
UPDATE Oct 2022: A new discussion on statistical power, MDE, and planning A/B tests has been published, which addresses the issues discussed in this installment, and more.