Can running multiple A/B tests at the same time lead to interferences that result in choosing inferior variants?
Does running each A/B test in a silo improve or worsen the situation?
If there is any danger, how great is it and how much should we be concerned about it?
In this post, I’ll try to answer these questions with regards to conversion rate optimization and UX A/B testing, but the conclusions should be generalizable to E-mail testing, Landing Page Optimization and other areas where randomized controlled experiments are used online. The key takeaways are conveniently listed near the end of the post, so you can scroll down if you are looking just for straight up “do’s and don’ts”.

To set the stage, let’s assume we have two simple A/B tests: T1 and T2. T1 is on the cart page, T2 is on the checkout page.
For the sake of simplicity, let’s assume that both A/B tests have the same primary endpoint and measure the success or failure of tested variants based on e-commerce transaction rate.
When faced with the task of running 2 or more tests on the same website, an A/B tester may choose between these possibilities:
A.) Run the tests in parallel, without worrying about any interference between them
B.) Run the tests in parallel, but on isolated audiences (the audience experiencing test T1 will not participate in test T2, and vice versa)
C.) Run the tests one after another: once T1 has concluded, T2 can start.
Obviously, option C is the safest, but will significantly throttle the capacity for running A/B tests. Is it then justified to choose option C in order to avoid any interference, despite the great cost? Is option B better than option A? Is running the tests in parallel and not caring about interference just as good as running them one after another?
Before continuing to review the different options one by one, we need to deal with
Time Overlap Scenarios with Concurrent A/B Tests
The possible scenarios in terms of test overlap in time are:
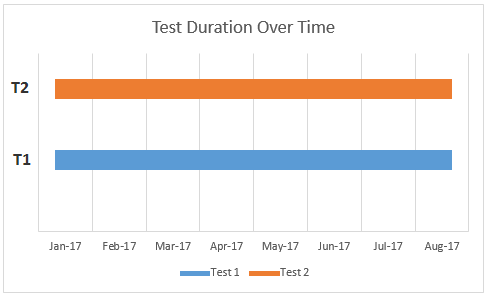
1. T1 and T2 are both run exactly at the same time – complete overlap.
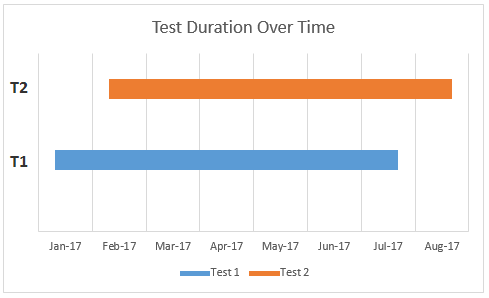
2. T1 starts before T2 and ends before T2, with significant overlap.
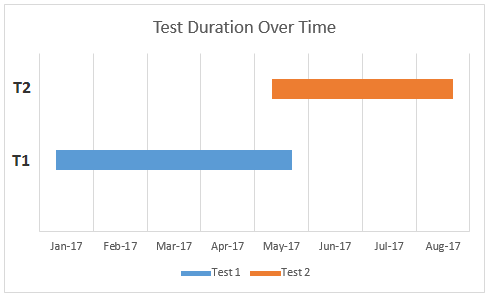
3. T1 starts before T2 and ends before T2, with minimal overlap
4. T1 starts before T2 and ends after T2:
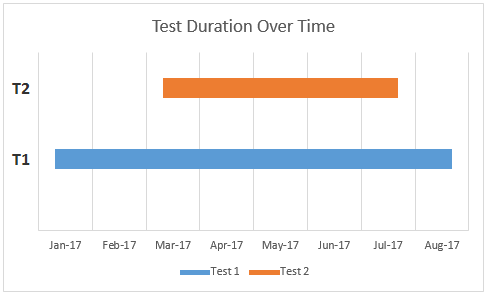
which is also equivalent to the case where T1 and T2 start at different times, but end at the same time.
5. There is no overlap in time.
Of course, in 2,3 & 4 the T1 and T2 could be swapped, which increases the total number of hypothetical situations to 8, but sticking to the five scenarios above doesn’t decrease the generalizability of our conclusions so let’s stick to them. It is obvious that time scenarios 1-4 are applicable to both Option A and Option B, while scenario 5 is exactly Option C.
Let’s simplify things a bit more by adding the assumption that once a test is completed, the winner is chosen and continues to run from that point onwards. If it is not possible to immediately “hard-code” a test winner, the A/B testing delivery software would usually be left running with 100% of users being served the winner, until the changes can be permanently implemented.
It is easy to see that if one is doing fixed-sample tests (classical statistical significance tests), then the calculations are very easy, as we only need to consider the % of the time the two tests were running together (overlap time) and then multiply it by the effect of T1 on T2 and vice versa. So, in effect, a shorter than 100% overlap time will mean that we’d need to discount any interference by Test 1 on Test 2, and vice versa, by the difference between 100% and the % of overlap time.
Since this is equivalent to just discounting the effect, we do not need to consider the first four time scenarios as different, we can just consider the simplest one: 100% time overlap and the results will be generalizable to all four.
With the more efficient sequential tests such as ones using the AGILE A/B testing method the math is more complicated, but I believe the same logic can be applied, so no special attention will be given to that case in this post, as the results should apply equally.
Concurrent A/B Tests: To Isolate or Not to Isolate?
This is the easiest one to tackle, so that’s why I start with it, instead of the interference question.
First, running tests in parallel isolated lanes (testing silos) doesn’t really make sense from an efficiency standpoint. With any given number of users or sessions, it would take just as much time to run two tests in isolated lanes as it would take to run them one after another. If you have 10000 users per month and need to run two tests, each requiring 5000 users, then it makes no difference how you slice the users: by time or in silos, it would still take 1 month to run the test. Given that Option C is unquestionably a safe one, it would be the preferred choice over option B.
Then there is a clear downside for option B: running experiments in isolated lanes is sure to miss testing some of the possible interactions between the tested variants.
Having separate testing lanes would be equal to running a test on desktop users, and then releasing the winning variant to desktop and mobile users. Surely, the effect for mobile users might be the same as for desktop users, but there might be a significant negative or positive difference.
If you are not sure about the above, consider the following scenario, where version A is the control and version B is the tested variation for two parallel experiments.
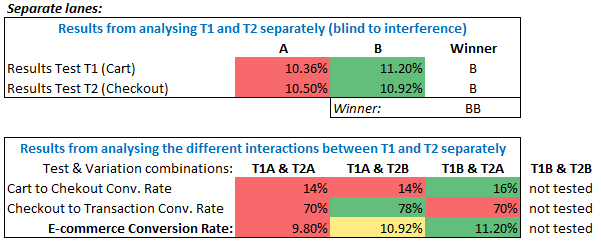
The first table is how the results would look like when analyzing the tests. The second table shows what combinations of the variants from both tests would have been tested in reality.
As you can see, in this case the winner is in fact T1B (variant B from Test 1) and T2B (variant B from Test 2). No users have been exposed to this combination during the test, so by following our tests’ conclusions we would be releasing an untested experience! We wouldn’t know how this combination would perform – it might be the same as what we tested, or it could be better or worse. Had we run the same test using approach A.), we would have correctly identified T1B and T2A as the winning variants.
To illustrate this further, if the tests are siloed, user allocation would look like so:
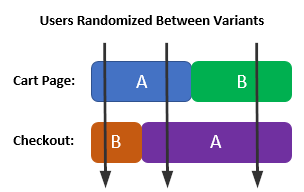
It is clear that no users will experience B-B.
If the experiments are not siloed, user allocation would look like so:
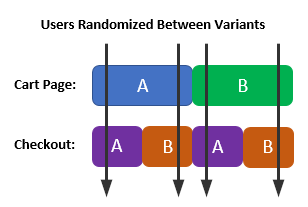
It is clear that about ¼ of users would experience B-B.
To sum up: using Option B can result in an untested user experience being released to production and it offers no efficiency gains compared to an option that doesn’t have that drawback (C), so it is clear that running tests in separate testing lanes should not be done.
The answer to the question “Does running each A/B test in a silo improve or worsen the situation?” is: it worsens it.
The above is true not only for the case where both tests start and end at the same time, but also for any of the other possible cases, which we’ll examine below.
Should We Worry About Test Interference?
Basically, if we choose to go with Option A – running tests in parallel with no isolation, is it justified to ignore potential interferences? As stated initially: “Can running multiple A/B tests at the same time lead to interferences that result in choosing inferior variants?”
I chose to answer this with a simulation. Its design is detailed separately below the post* for those interested in the details, but it basically simulates random interactions between the two variants of the two tests (4 total interactions) and then checks if analyzing the tests blind to the interactions would yield outcomes different than the correct ones.
Running 1000 simulated experiments, 323 (32.3%) resulted in picking the wrong variation for one of the two tests. 0 (0%) cases resulted in picking the wrong variation on both tests. In all cases only one of the winners was the wrong one, but this doesn’t make the error less bad, since sometimes the chosen combination will have the worst or second worst performance of the four. Please, note that the above simulation checks only if it is possible to run into such issues and says nothing about their prevalence or likelihood, we’ll deal with that in the next part.
So, it is theoretically entirely possible for interference between the two tests to yield results different than the correct ones.
Here is one such a theoretical scenario in detail:
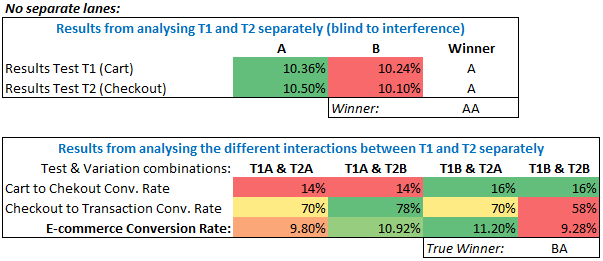
What is happening is that the interaction between T1B and T2B is stronger than the interaction between T1B and T2A, and it is opposite in sign to the interaction between T1A and T2B, thus making the overall T1B result worse than T1A. Thus, an inferior combination would be chosen if the tests are examined separately, without specifically examining the interaction between the two tests.
If there is a stronger and opposite in sign interaction in two of the four possible combinations in our A/B testing scenario, we are virtually guaranteed to get the result of one of the two concurrent A/B tests wrong.
This can be explained in another way if we replace one of the test’s variants with a user segment, say, based on country. So instead of Test 1 being an A/B test with variations A and B, let it be a segmentation of our users into US and non-US users.
Now the question becomes, essentially: is it possible for Test 2 to have a such a negative influence on US users that it negates the positive influence it has on non-US users, so that in the end we would find evidence that the tested variant is no better than the control for our audience as a whole?
Sure, such things happen every day which is why it is a good practice to examine how major subsets of users are affected by a test variant (seeking statistically significant results there is another matter, deserving of a separate post). No amount of randomization and evening out can overcome this effect. If such an effect is found, subsequent tests can be run separately on the two segments and separate solutions can be implemented. In some cases, the difference might be so strong, that the decision to implement for a given segment, or to not implement for another, can be made on the spot.
To get back to A/B tests, if an analysis of the interaction between two tests reveals a strong interference, then it can be examined and the proper decision can be made, similar to how we would do if we recognize that an A/B test we are running works great for our US visitors, but fails abysmally for our non-US ones.
To conclude this part, the answer to the question “Can running multiple A/B tests at the same time lead to interferences that result in choosing inferior variants?” is a resounding “Yes”.
How Likely is Interference in Concurrent A/B Tests & What Impact Can It Have?
This is, without a doubt, the hardest question to answer. I don’t really think an answer is possible, since it would require prior knowledge about the likelihood and magnitude of interference between tests. Or, it would require knowing the true distribution of A/B test results and the differences that choosing a wrong one makes.
Who can say how often will we see a stronger and opposite in sign interaction in two of the four possible combination in our A/B testing scenario, and how big the difference between the chosen variants and the best variants will be? If we knew that, it would make no sense in running A/B tests, as we already have all the knowledge we are seeking to obtain through an online experiment.
With that said, I think this question can be partially explored through more simulations, but the parameters for these would have a great impact on the results. It could be an interesting exercise to run several simulations with different parameters to see the impact of the parameter values, however there is no guarantee that their results will match reality in general, or that they would be useful to any particular domain of A/B testing application.
In short, there is no certain way to establish the likelihood of harmful interference between concurrent A/B tests, nor the impact of such events.
Takeaways on Running Concurrent A/B Tests
#1. Running multiple A/B tests at the same time can theoretically lead to interferences that result in choosing an inferior combination of variants. Given that from two combinations of variants one has a stronger and opposite sign interaction than the other, it is guaranteed to happen.
However, this is not unique to running concurrent online experiments, as it can happen with any two (or more) segments of the tested population. The way to avoid it is to examine the interactions between any two sets of A/B tests as if examining the effect of a single A/B test on different subsets of the website visitors. Action can then be taken accordingly.
#2. Running each A/B test in isolated lanes (silos) can lead to releasing untested user experiences, so it should be avoided whenever possible. Furthermore, it offers no performance benefits compared to running the same tests one after another.
#3. Estimating the likelihood that any tests might interfere with each other in a detrimental way and estimating the impact of making bad choices due to running concurrent tests is, I believe, not possible. It is left to the common sense of the experiment lead to screen the released tests for possible strong interactions in either direction and make sure obvious negative interactions are not allowed. I recommend doing post-test segmentation of the results by A/B test variation exposure whenever possible.
Possible Future Work
It will be interesting to explore how the likelihood of wrong inferences purely due to increasing the number of concurrent tests changes when we do the same simulation with 3 or more concurrent tests, but this is work for another time.
* Simulation Design
For the simulation, we need to generate random outcomes for all 4 possible variants: T1AT2A, T1AT2B, T1BT2A, T1BT2B. Assumptions about the distribution of those outcomes are inevitably going to be question, but I think it is fair to say that both real improvements of over 50% as well as real losses of over 50% are very unlikely, given the tests are properly QA-ed before launch. With that in mind, the randomly generated true outcomes are from a uniform distribution that is bound by -50% of the control value at one end and +50% the control value on the other.
If we set the baseline for the cart to purchase complete conversion rate at 40%, we get a range for the true rates of 20% to 60%.
Even if this assumption is not true, it will not influence the conclusion for question #1, which is whether any kind of interference can lead to a wrong result. It only affects the answer to question #3 – how great the danger of making a bad call is and how much we should be concerned with it.
Now, while the true outcomes will be randomly generated, the simulation will be blind to those outcomes. It will evaluate experiment 1 and experiment 2 separately, calculating statistical significance and determining a winner from each of the two tests. These two winners are then compared to the actual true winners to determine whether the conclusion was correct or not.
When evaluating the results from the simulation we need to remember that some true winners will be missed due to type II errors, while some losers will get mistaken for winners due to type I errors. Just a reminder, the former is controlled via statistical power, while the latter – via statistical significance.



