One-tailed vs Two-tailed Tests of Significance in A/B Testing

The question of whether one should run A/B tests (a.k.a online controlled experiments) using one-tailed versus two-tailed tests of significance was something I didn’t even consider important, as I thought the answer (one-tailed) was so self-evident that no discussion was necessary.

However, while preparing for my course on “Statistics in A/B Testing” for the ConversionXL Institute, an article has come to my attention, which collected advice from prominent figures in the CRO industry who mostly recommended two-sided tests over one-sided tests for reasons so detached from reality and so contrary to all logic, that I was forced to recognize the issue as being much bigger than suspected. The fact that almost all known industry vendors are reported as using two-sided tests either by default, or as the only option made me further realize the issue warrants much more than a comment under the article itself if I am to have any chance of properly covering the topic.

Vendors using two-tailed tests according to the ConversionXL article (Jul 2015), include: Optimizely, VWO (Visual Website Optimizer), Adobe Target, Maxymiser, Convert, Monetate. A vendor I can guarantee is using a one-tailed test: Analytics-Toolkit.com with our A/B Testing Calculator and Statistical Significance and Sample Size Calculators. Since you are reading this on our blog, it should be obvious what side of the debate I’ll be on here. I actually intend to go all the way and argue that barring some very narrow use-cases, one should never use a two-tailed statistical test.

UPDATE (Aug 8, 2018): It turned out the issue is much bigger than the A/B testing industry so I launched the “One-Sided Project” featuring a dozen or so articles on one-sided statistical tests, links to relevant literature, simulations, etc. I highly recommend checking it out!

Before I continue, I should note that the terms “two-tailed” and “two-sided“, “one-tailed” and “one-sided” are used interchangeably within the article. Also, I specifically refer to z-tests, which are the most appropriate significance tests for most A/B testing data (difference between proportions), but what is said is also true for t-tests. Part of the discussion should be taken with caution with regards to tests with non-symmetric distributions, such as F-tests, Chi square tests, and others.

Misconceptions on Two-tailed vs One-tailed tests

In the article, and elsewhere, two-tailed tests are described as:

• leading to more accurate and more reliable results
• accounting for all scenarios
• having less assumptions
• generally better

In contrast, one-tailed tests, allegedly:

• enable more type I errors
• only account for one scenario
• can lead to inaccurate and biased results
• or at least do nothing to add value (vs. a two-tailed test)

Sadly, the above misconceptions are not limited to the conversion optimization/online testing community, but spread across scientific disciplines, as evident by some papers I’ve examined while writing this article. Some^[3] of them suggest that researchers should clearly justify why they used a one-tailed instead of a two-tailed test, as if a one-tailed test is some very special animal that should be approached carefully and only with proper reason. “Are one-tailed tests generally appropriate for applied research, as many writers have implied? We believe not.” state others^[1], despite leaving some wiggle room for their use.

It is only fair to note that a comment in the same article mentions how easy it is to convert from one-tailed to two-tailed tests and vice versa (assuming a symmetrical binomial distribution), but that doesn’t address the real point of distinction at all. A single benefit was listed by Kyle Rush, saying that it requires less users to produce significant results when compared to a two-sided test at the same significance threshold, without any explanation why. This last one, I believe, is what a lot of people mistakenly believe leads to the test resulting in more type I errors, but we’ll get back to this point in a minute. The article ends with Chris Stucchio’s advice, which is actually the soundest of all, but way too ambiguous to alleviate the issue.

Where do the misconceptions come from?

The misconceptions and resulting misuses of two-tailed tests are widespread, as Cho & Abe^[2] note in their recent paper on statistical practices in marketing research, published in a journal for business research:

“This paper demonstrates that there is currently a widespread misuse of two-tailed testing for directional research hypotheses tests.”

(Emphasis mine.) Why are such misuses so widespread?

Firstly, they come from really bad advice given in all sorts of statistical books, posts and discussions. Take Wikipedia, for example:

“A two-tailed test is appropriate if the estimated value may be more than or less than the reference value, for example, whether a test taker may score above or below the historical average. A one-tailed test is appropriate if the estimated value may depart from the reference value in only one direction, for example, whether a machine produces more than one-percent defective products.”

(Emphasis mine.) The page itself offers a somewhat cogent explanation of the difference between the two types of tests, but the above quote is utterly misleading.

A more explicit phrasing of the above can be found on a Q&A page, supposedly written by someone who understands statistical testing in Psychology, which is a discipline close to conversion rate optimization as it deals with human behavior and has more loosely defined hypotheses than, say, physics:

“A one-tailed hypothesis, or directional hypothesis, predicts the actual DIRECTION in which the findings will go. It is more precise, and usually used when other research has been carried out previously, giving us a good idea of which way the results will go e.g. we predict more or less, an increase or decrease, higher or lower.

A two-tailed hypothesis, or non-directional hypothesis, predicts an OPEN outcome thus the results can go in 2 directions. It is left very general and is usually used when no other research has been done before thus we do not know what will happen e.g. we predict a difference, an effect or a change but we do not know in what direction.”

(Emphasis mine.) I cite it not because it is a hugely influential source (although that answer was viewed over 6000 times), but because it sums up nicely and clearly the bad advice I’ve seen in countless other places.

Secondly, the issue is worsened by committing the common mistake of treating statistical significance as a probability attached to a particular hypothesis, not the testing procedure, as it really is. In other words, it’s the error of treating a p-value of 0.05 (95% significance) as the probability that your hypothesis is true, and vice versa: treating a low significance as proof that your hypothesis is false. If you need a refresher on the topic, be sure to check out my complete guide to statistical significance in A/B testing.

What would you think if you had the above idea about statistical significance and were faced with such an example:

An A/B test is conducted, testing a control (Variant A) versus another version (Variant B). Each variant is experienced by 10,000 users, properly randomized between the two. A converts at 20%, while B converts at 21%. The resulting significance with a one-tailed test is 96.01% (p-value 0.039), so it would be considered significant at the 95% level (p<0.05).

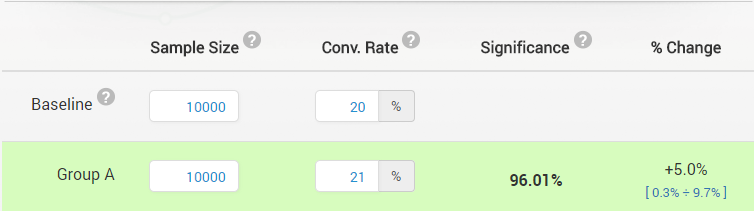
Now, using the same numbers, one does a two-tailed test. “Surprisingly”, the result is now 92.2% significance (p-value 0.078) and is no longer significant at the 95% level! What is going on here? Since a one-tailed test returns a higher significance (lower p-value), given the same data, it must be a less stringent test, right? If it is easier to get a higher significance level from a one-sided test, then it must be more error prone than a two-sided test, thus less reliable and leading to inaccurate results, as some have stated, right? Right?

WRONG!

Two-sided tests explained

To even understand the existence of the two types of tests, a refresher on the use of significance tests would be helpful. Significance testing is used as a part of a decision procedure, where it is decided prior to the test what would be tested and what the evidential threshold would be. That is the so-called significance threshold or confidence threshold. Textbook examples use 95% (0.05), but there is nothing special about that number, and values much higher, or much lower than that can be used depending on the particular risk-adjusted costs and benefits. What we generally want to ward against is committing the error of mistaking “random” variance, or noise, for real effect (type I error), or mistaking the presence of variance for lack of real effect (type II error).

To make sure stakeholders, whether businesses or other organizations, are on board and that the test will lead to a certain action, it is useful to define decisions, associated with crossing the evidential threshold, or not crossing it. Most often there is a commitment to performing a given action if the threshold is crossed, e.g. implement a new variant of our shopping cart page, while committing to not do that same action if the threshold is not crossed, out of fear of breaking what is already in place and working to some satisfaction.

In such a framework the null hypothesis is a state of the world to be avoided and warded against. It is what we want to make sure is not true, to a degree controlled by the evidential threshold. In light of this:

A two-sided hypothesis and a two-tailed test should be used only when one would act the same way, or draw the same conclusions, if a statistically significant difference in any direction is discovered.

Think about it for a second. How often would one do that in A/B testing, be it in conversion rate optimization, landing page optimization, e-mail optimization, etc.? How often does one define a hypothesis in this way: “our new shopping cart performs differently than our existing one and take the same action would be taken if it is better or worse. Therefore, our null is that the new shopping cart performs exactly as the existing one”? How often would one act the same way if your new e-mail template is better than the existing one, and if it is worse?

There are some scenarios when you would do the same immediate action, e.g. stop a production line if some measurement of the produced good goes too much in either direction, but even in such cases you would want to know in which direction it deviated so you can apply the appropriate fix. However, a two-sided hypothesis doesn’t allow you to say anything about the direction of the effect.

In using a two-tailed test, you can commit any of three errors:

Type I error: rejecting the null hypothesis when it is true, e.g. inferring your new shopping cart is different, when it is the same. Controlled by statistical significance.

Type II error: failing to reject the null hypothesis when it is false, e.g. inferring your new shopping cart is not different, when it in fact is. Controlled by statistical power.

Type III error: where you use a two-sided hypothesis and a corresponding two-tailed test of significance to make any declaration about the direction of a statistically significant effect. This error is not explicitly controlled, as the test is not meant to be used in such a way.

Bells should be ringing out loud about what is wrong in using two-tailed significance tests for most if not all practical applications in A/B testing. The same holds for most other spheres where statistical inference is done.

This will be reviewed in more detail below, but first, a word about

One-sided tests

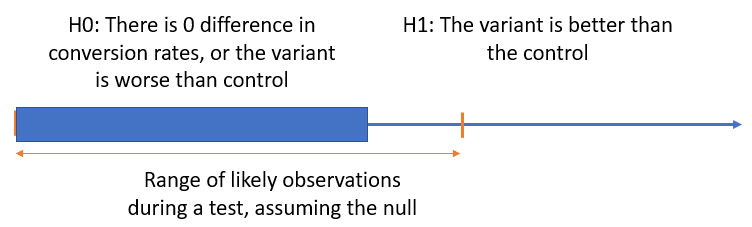
One-sided hypotheses are directional by design. For example, when planning the A/B test one decides that a certain action will be taken if the result is better performance, and in another way if it is equal to or worse performance compared to the control, based on some metric, say e-commerce conversion rate. This is a right-sided alternative hypothesis (left-sided null). A left-sided alternative would be that one would act in a certain way if the result is worse, and act in another way if it is equal to or better than the control. So, in both of these cases one fears that the results fall on one of the sides. In the graph below it is a negative true performance that one fears when considering whether to implement our new shopping cart, or not:

In light of this:

A one-sided hypothesis and a one-tailed test should be used when one would act a certain way, or draw certain conclusions, if a statistically significant difference in a particular direction is discovered, but not if a difference is discovered in the other direction.

Note that the words “predict”, “expect”, “anticipate”, etc. are nowhere in the definition of a one-tailed test. That’s because in a one-tailed test one does not assume anything about the true effect. A one-sided hypothesis says something about our intentions and decisions following the test, not about the true performance of any of the tested variants!

The real difference between one-tailed and two-tailed tests

The most important distinction between the two tests is our intentions: what one aims to find during the test and what actions would follow a statistically significant result. If our actions would be the same, regardless of the direction of the effect, then sure, use a two-tailed test. However, if you would act differently if the result is positive, compared to when it is negative, then a two-tailed test is of no use and you should use a one-tailed one.

Why is it then that it is easier to get a significant result from a one-tailed test compared to a two-tailed one? Why is 95% significance from a one-tailed test equal to only 90% significance in a two-tailed test? The short answer is: because they answer different questions, one being more concrete than the other. The one-tailed question limits the values one is interested in, so the same statistic now has a different inferential meaning, resulting in lower error probability, hence higher observed significance. Declaring one would act the same if the result is in either direction results in an increase of the range of values one is interested in rejecting, resulting in a higher probability that one would be in error by using such a decision rule, hence the lower significance.

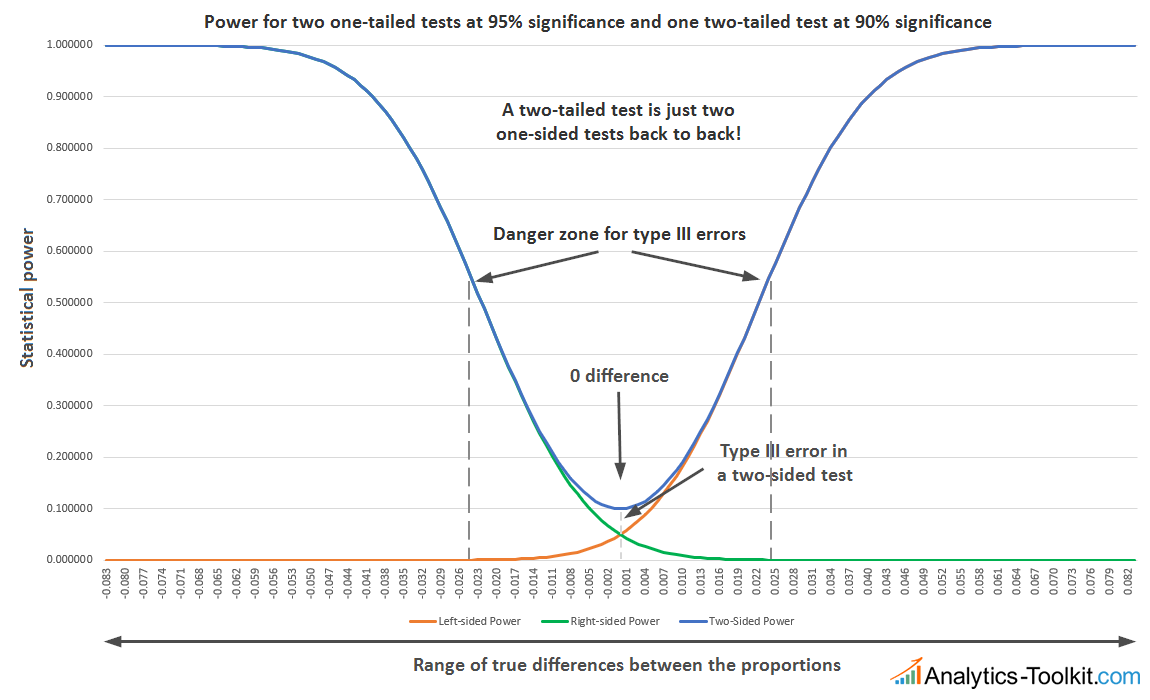
The longer explanation I can offer is via statistical power, specifically how it is distributed in a two-tailed vs one-tailed test. As you know, statistical power is the probability of detecting a statistically significant effect of a given magnitude, if it truly exists. In terms of power, a two-tailed test is just two one-sided tests, back to back (remember, symmetrical distributions are assumed), like so:

Two-tailed vs two one-tailed tests, side = where the null is (click for large version)

The power function of the two-tailed test over the possible true differences between our conversion rates is just the sum of the power functions of the two one-sided tests. Therefore, power is symmetrical in both directions, unlike a one-tailed test, which only has power in one direction. Thinking about a two-tailed test as composed of two one-tailed tests, one in each direction, it is obvious that one needs to consider the combined power of the two tests, which leads to an increased type I error (alpha), assuming the sample size and effect size of interest are the same.  It is this added power that lowers the significance of the two-tailed test, as even when observing a positive statistically significant result, it could have come from a true negative. The difference in power is captured in the small area enclosed between the three power functions (see graph).

Say a positive relative difference of 10% with a p-value of 0.1 (90% significance) is observed in a two-tailed test. What does that really mean? It means there is 10% probability that such an extreme result could have been observed even if there was no difference in either direction. Note that one does not know the direction, yet, even though the difference is positive. There is no clear measure of the type III error, that is, the sign error, in such a scenario.

Now, let’s say two one-sided significance tests are performed. The left-sided one would produce a p-value of 0.05 (95% significance), meaning that there is 5% probability to observe such an extreme result in the positive direction or a more extreme one, if there was no true difference, or the true difference was in the negative direction. This corresponds to a type I error of 5%. The right-sided one, though, would produce a p-value of 0.95 (5% significance), meaning that there is 95% probability to observe such a positive result or a more extreme one if there was no difference, or the difference was in the positive direction.

Since the two one-sided tests completely exhaust the possible set of true differences, the possibility of a type III error in each one-sided test is now exactly equal to their type I error, so there is no need to speak of type III errors exclusively. For the left-sided test that number is 5%, meaning there is only 5% probability of observing such a result, if the conversion rate of our variant is worse than or equal to control. Same for the right-sided test, where there is 95% probability of observing such a result, if the conversion rate of our variant is better than or equal to control.

See this in action

Try itStatistical Significance Calculator
Robust p-value and confidence interval calculation.

If thinking in confidence intervals is easier for you (I think it is for most people in A/B testing), then consider that a 90% confidence interval from a symmetrical error distribution is equal to the overlap of two one-sided intervals at 95% confidence. Looking at the 90% confidence interval will surely protect you from a type III error and it is exactly equivalent to looking at a one-sided 95% confidence interval in either direction. Going back to the example this article began with, note that next to the 96.01% significant result there is a 90% confidence interval that covers [+0.3% – +9.7%], clearly illustrating the equivalence between the two.

To conclude – since two-tailed tests are basically two one-sided tests stuck together, there is absolutely no basis for claiming any of them is more or less accurate. They are both accurate, but answer different questions.

One-tailed and two-tailed tests are equally accurate, but answer different questions.

Therefore, most of the time the issue is with the application of two-tailed tests of significance: they are too often employed to answer questions that can only be answered by a one-tailed test.

Debunking the myths

The myths are mostly debunked above, but let’s state them explicitly for more clarity.

Two sided tests do not have less assumptions than one-sided tests. They do not account for different scenarios than one-sided tests (more, or less scenarios). They do not lead to more accurate and more reliable results, in fact, given they are more open to misinterpretations due to type III errors, they may be more likely to lead to incorrect conclusions.

Since they are the same thing, claiming any such benefits of two-tailed tests over one-tailed ones would be like saying that a thermometer’s accuracy or reliability depends on what you plan on doing with a temperature reading. Let’s say the reading is 30.5 degrees. If you are only interested if the temperature is above 30 degrees the reading would not be less accurate than if you were interested in the temperature being exactly 30 degrees. The thermometer is equally accurate in both cases, but depending on what you care about, you can interpret it differently. If you know that it has an error margin of 0.6 degrees in each direction, then you know that it is much more likely it came from a true temperature higher than 30 degrees than from a temperature below 30. It’s your action depending on the reading that matters. The reading itself is, naturally, not affected.

This means that it is utterly ridiculous to claim one-tailed tests somehow enable more type I errors, or that they can lead to inaccurate or biased results. If they can, then so can a two-sided test on the same data. If you still don’t believe me: run some simulations. I’ve ran hundreds of thousands of them in the past years and I can tell you that the error rate of one-tailed tests is conservatively maintained in all possible scenarios for the underlying true value.

Saying they only account for one scenario is false as well: they make no predictions about what the true value is. A one-tailed test takes all possible true values into account, then tells you something about the probability of the true effect being in the direction you are interested in. If you are interested in the other direction, just run the opposite one-sided test. For symmetrical error distributions this is equivalent to subtracting the observed significance from 1 (or 100%).

See this in action

Try itA/B Testing Calculator
Advanced significance & confidence interval calculator.

Comments that one-tailed tests “do nothing to add value” versus two-tailed tests demonstrate ignorance about the possibility of type III errors and of the connection between a research hypothesis and a statistical hypothesis, and can only be understood if one means that both procedures are equivalent, but that is not the meaning I got out of the context of the whole statement.

The above is true whether you apply it to A/B testing where you want to check a new checkout flow vs the existing one, or to medical testing, where you test if your treatment is better than current practices, or to physics, where you test in which direction the existing model of the physical building blocks and forces among them doesn’t hold. Even when requirements in official statistical guidelines are written in terms of two-tailed tests, this doesn’t mean they can’t be easily translated into stricter one-tailed tests in either direction, without a statistical penalty of any sort.

One-tailed tests should be preferred over two-tailed tests

There are two sides to the discussion here, one is the planning stage, the other is the observation/analysis stage.

For the planning stage, given that a hypothesis is clearly established and there is agreed upon action that will be taken if a particular evidential threshold is met, I see no reason to plan for two-sided tests at all. I think it is clearer when a one-sided hypothesis is used instead, since the direction of the effect is explicitly stated. If you still would like to consider three possible actions, depending on the three possible outcomes: non-significant, positive significant, negative significant, then do so explicitly by defining two one-sided hypotheses, then power the test (calculate the required sample size) based on a one-tailed test.

The benefits from doing so are clear: in order to reliably detect a given effect with 95% two-sided significance, one needs 20-60% higher sample size than to detect the same effect at 95% one-sided significance. Same baseline in both cases. 20% is when the required significance is in the higher 90s, while 60 is when it is in the 80-90% range, it is even higher at lower ranges of significance thresholds. Why commit to 20-60% slower tests to answer a question you didn’t ask and the answer to which would make no difference?

At the analysis stage when the direction of the result is clear I see no reason not to conduct two one-tailed tests with regards to the reported p-value (observed significance), especially in A/B testing where the distributions are usually symmetric, so one complements the other. I think it is also better to report confidence intervals not as 90% two-sided, but as an upper/lower 95% one-sided interval or two 95% one-sided intervals back to back, since this is what users really want to ask of the data. Why hide the evidence and artificially lower the reported confidence interval threshold by calculating it under a hypothesis most no one cares about? Why consider a type III error, when you should only be considering the errors the users care about, in which case type III and type I coincide?

Why use two-tailed tests that potentially open the practitioner up for the fallacy of committing an error of the third kind (type III error) and mistaking a significant result in one direction as evidence that the effect is in that direction? Let the user know what the data says in the direction he or she cares about. Make it so the statistics answer the questions asked.

References

1 Hurlbert, S.H., Lombardi, C.M. (2009) “Misprescription and misuse of one-tailed tests”, Austral Ecology 34:447-468
2 Hyun-Chul Cho Shuzo Abe (2013) “Is two-tailed testing for directional research hypotheses tests legitimate?”, Journal of Business Research 66:1261-1266
3 Ruxton, G.D., Neuhäuser, M. (2010) “When should we use one-tailed hypothesis testing?”, Methods in Ecology and Evolution 1:114–117

About the author

Georgi Georgiev

Managing owner of Web Focus and creator of Analytics-toolkit.com, Georgi has over twenty years of experience in online marketing, web analytics, statistics, and design of business experiments for hundreds of websites.

He is the author of the book "Statistical Methods in Online A/B Testing", of white papers on statistical analysis of A/B tests, and has been a speaker at conferences, seminars, and courses. Georgi has been distinguished as a winner in the Data & Analytics category of the 2024 Experimentation Thought Leadership Awards.